Regression#
Introduction to Regression
This is an introduction to regression analysis, a statistical method used to examine the relationship between one dependent variable and one or more independent variables.
Regression models in pattern recognition are powerful tools for understanding data patterns, making estimations and predictions, and are essential across a wide range of applications in various domains.
In this context, the linear model describes the data as \( D = \{\mathbf{x}_i, y_i; i=1, \cdots, n \} \). Reviewing all the work in pattern recognition, we aim to model data using either linear or non-linear forms, in both supervised and unsupervised learning scenarios. The emphasis of this book is on the cost function, as minimizing the cost function leads to discovering the most desirable model. Additionally, solution methods are needed to solve the minimization problem, which can be approached in either an online or offline manner.
As shown in the figure above, regression and clustering are similarly effective; the only difference lies in the dataset used. Clustering provides indices in the form of centers or boundaries, while regression offers linear or nonlinear equations to represent data indices, making it quite similar to clustering.
Regression refers to a statistical method used to model the relationship between a dependent variable (often denoted as \( y \) ) and one or more independent variables (often denoted as \( x_1, x_2, \ldots, x_p \) ). The goal of regression analysis is to understand how the dependent variable changes when the independent variables are varied. It is primarily used for estimation continuous or numerical outcomes.
Regression Models#
Regression models are mathematical equations that describe the relationship between variables. These models aim to estimate the value of the dependent variable based on the values of the independent variables. There are various types of regression models, including:
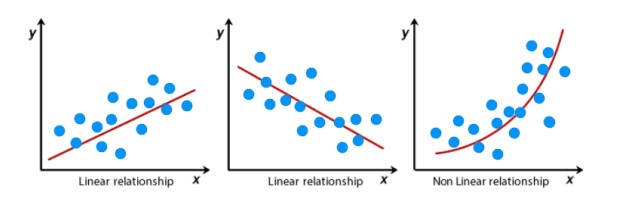
Linear Regression: Assumes a linear relationship between the dependent variable and the independent variables.
Non-Linear Regression: Models non-linear relationships such as higher-order polynomial terms.
Data Collection for Regression Tasks in Pattern Recognition#
Effective data collection is crucial for building accurate and reliable regression models in pattern recognition. Such as economics, healthcare. We use UCI Machine Learning Repository, Kaggle, Internet of Things (IoT) devices (For instance, smart home devices, environmental sensors, and wearable health monitors), Data from stock markets, Data from platforms like Twitter, Facebook.
